"蔚来杯"2022牛客暑期多校训练营4¶
| 排名 | 当场过题数 | 至今过题数 | 总题数 |
|---|---|---|---|
| 25/1452 | 9 | 14 | 14 |
A¶
solved by JLK
题意¶
给定\(n\),有两个长度为\(n\)的数组\(w_i,p_i\),从中选\(m\)个任意排列得到\(a_i\),使得\(\sum\limits_{i=1}^m w_{a_i} \prod\limits_{j=0}^{i-1}p_{a_j}\)最大。
\(1 \le n \le 10^5,1 \le m \le \min\{n,20\},1 \le w_i \le 10^9,0.8 \le p_i \le 1.2\)
题解¶
相邻交换法。
对于两个元素\(x,y\),\(x\)排在\(y\)前面要满足\(w_x+w_yp_x \gt w_y+w_xp_y\)。
也就是\(w_y(p_x-1)-w_x(p_y-1)\gt 0\)。实际上是一个叉积的形式。把每个点看成\((p_i-1,w_i)\),相当于是逆时针排序。而所有点都在\(x\)轴上方,不会出现环的情况。也就是说这个关系是全序,可以sort。
排序完之后还需要取\(m\)个点,直接dp即可。
\(O(n\log n+nm)\)
B¶
**upsolved by **
题意¶
题解¶
C¶
solved by TYB
题意¶
给出\(w\),\(q\)次询问长度为\(n\)的仅包含\([0,w)\),且数字\(i\)至少出现\(c_i\)次的数字串个数(对于每个询问\(c\)都一样)。
\(2\le w<10,q\le300,\sum_{i=0}^{w-1}c_i\le50000,n\le10^7\)
题解¶
显然答案为\([\frac{x^n}{n!}]\prod_{i=0}^{w-1}(e^x-\sum_{j=0}^{c_i-1}\frac{x^j}{j!})\)。
\(n\)很大,无法直接卷积。考虑将其写为\(\sum_{i=0}^{w}e^{iw}g_i(x)\)的形式,由于\(g_i(x)\)只有\(\sum c\)项,只要预处理出每个\(g_i(x)\),就可以每次询问\(\mathcal{O}(w\sum c)\)暴力算\([\frac{x^n}{n!}]\)的系数。
设\(f_j(x)=\sum_{k=0}^{c_j-1}\frac{x^k}{k!}\),\(g_i(x)\)其实就是选\(i\)个\(f_j(x)\)乘起来的和。暴力预处理即可,复杂度\(\mathcal{O}(w^2\sum c\log(\sum c))\)。
D¶
solved by JLK
题意¶
有 \(n\) 个公司,第 \(i\) 个公司有 \(m_i\) 个工作,每个工作对三个能力分别有数值要求,必须三个能力都达标才能胜任这份工作。一个人只要能胜任一个公司的任意一份工作就可以去这个公司工作。
强制在线询问 \(q\) 次,每次给出三个能力的数值,问这个人可以去多少个公司工作。
\(1 \le n \le 10,1 \le m_i \le 10^5,1 \le q\le2×10^6\),能力的数值不超过\(400\)
题解¶
\(n\)很小,怎么写都行,用前缀和/前缀min/前缀或维护一下即可。
E¶
upsolved by JLK
题意¶
同D,\(1 \le n \le 10^6,1 \le m_i \le 10^6,\sum m_i \le 10^6\)。
题解¶
数据范围都变大了,只有能力值范围仍然很小,考虑预处理出每个能力值的答案(\(400^3=6.4\times 10^7\))。
每个公司相当于给答案里若干长方体的并的区域+1。
考虑维护这个区域。比较暴力的想法是枚举一维(看做一层一层的),剩下两维维护一下。
对于二维的情况,实际上产生贡献的区域是阶梯状的,按照其中一维从小到大枚举,另一维用类似单调栈的东西维护一下即可,这样就可以求出这一层的阶梯状区域。然后每两个台阶之间可以二维差分计算贡献。
而对于层,直接把每个工作都放到每一个能产生贡献的层里维护,也就不需要考虑三维的前缀和了。这样复杂度为\(O(400\sum m)\)。
加上求前缀和和询问,总复杂度为\(O(400\sum m+400^3+q)\)。
还有一种写法,是考虑三维前缀和的。按层数从小到大枚举,用set维护阶梯状区域。每一层会加入若干点,在set里面弹出被完全覆盖的点,再加入新点。弹出和加入的时候都需要维护三维的差分数组。具体来说,就是要考虑和相邻的两个台阶的交的区域,加入的时候只能贡献还没有被覆盖的区域,而删除的时候要把自己的区域减掉。而一个点如果没有被弹出,就可以贡献到后面的层,所以是三维的差分。
总复杂度为\(O(\sum m \log m+400^3+q)\),不过实测两种做法时间差不多。
F¶
upsolved by TYB
题意¶
\(n\)个点的树,每个点上有字符\(0/1\),\(q\)次询问两点路径组成的串有多少本质不同回文串。
\(n,q\le10^5\)
题解¶
回文自动机+树上回滚莫队。
先简要介绍一下树上回滚莫队。
首先是树分块。用王室联邦那题的方法进行树分块,若设定的块大小为\(B\),那么每块的点数在\([B,3B]\)范围内。此外,每个块还有一个属于它的关键点,这个关键点可能在块内也可能在块外,且对于任意块内的点,它到该块关键点的路径上所有点除关键点外,一定和它属于同一个块,这也表明了同块的点不一定是连通的。
那么,对于一个询问\((x,y)\),若\(x,y\)属于同一个块直接暴力,否则将这个询问分配给\(x\rightarrow y\)路径上经过的第一个关键点,可以发现,\(x,y\)所属块关键点深度较大的那个就是经过的第一个关键点。每次处理一个关键点的所有询问,将它们按\(dfn_y\)从小到大排序,维护一个右端点\(y'\)表示当前询问的\(y\)是什么,而左端点就是关键点。处理新的询问时先将\(y'\)移动到新的\(y\),完成右端点的移动,再把左端点移到新的\(x\),完成左端点的移动,求出答案,再把左端点的影响撤销。这就是树上回滚莫队的大致流程。
再考虑回文自动机。在移动右端点的时候,相当于在字符串后面加入一个字符,移动左端点时,相当于在字符串前面加入一个字符,还需要撤销(其实在移动右端点的时候也有撤销)。那么就要求回文自动机支持这些操作。
先考虑如何实现在字符串前端插入字符。类似在后端插入的思路,我们维护前缀回文串的相关信息。首先可以发现,大多数信息是无需额外维护的,由于自动机上每个节点都是回文串,一个回文串的非自身的最长回文后缀也是它的最长回文前缀。所以我们只需要维护当前串最长回文前缀的指针和最长回文后缀的指针即可。注意在头/尾插入字符的时候要考虑其对尾/头指针的影响,也就是整个串都是回文串的时候将两个指针设为相等即可。
再考虑撤销操作。回文自动机加入新节点时改变的信息不多,因此只要简单记录一下就可以了。但需要注意回文自动机跳fail的复杂度是基于势能分析的,当有撤销操作时复杂度就不对了。因此对于原来暴力跳fail的过程,我们考虑维护一个\(trans_{x,c}\)进行优化。它的含义是从\(x\)节点开始向上跳fail,第一个有\(c\)这个字符转移边的节点是哪个。这样复杂度就没问题了。
G¶
solved by JLK
题意¶
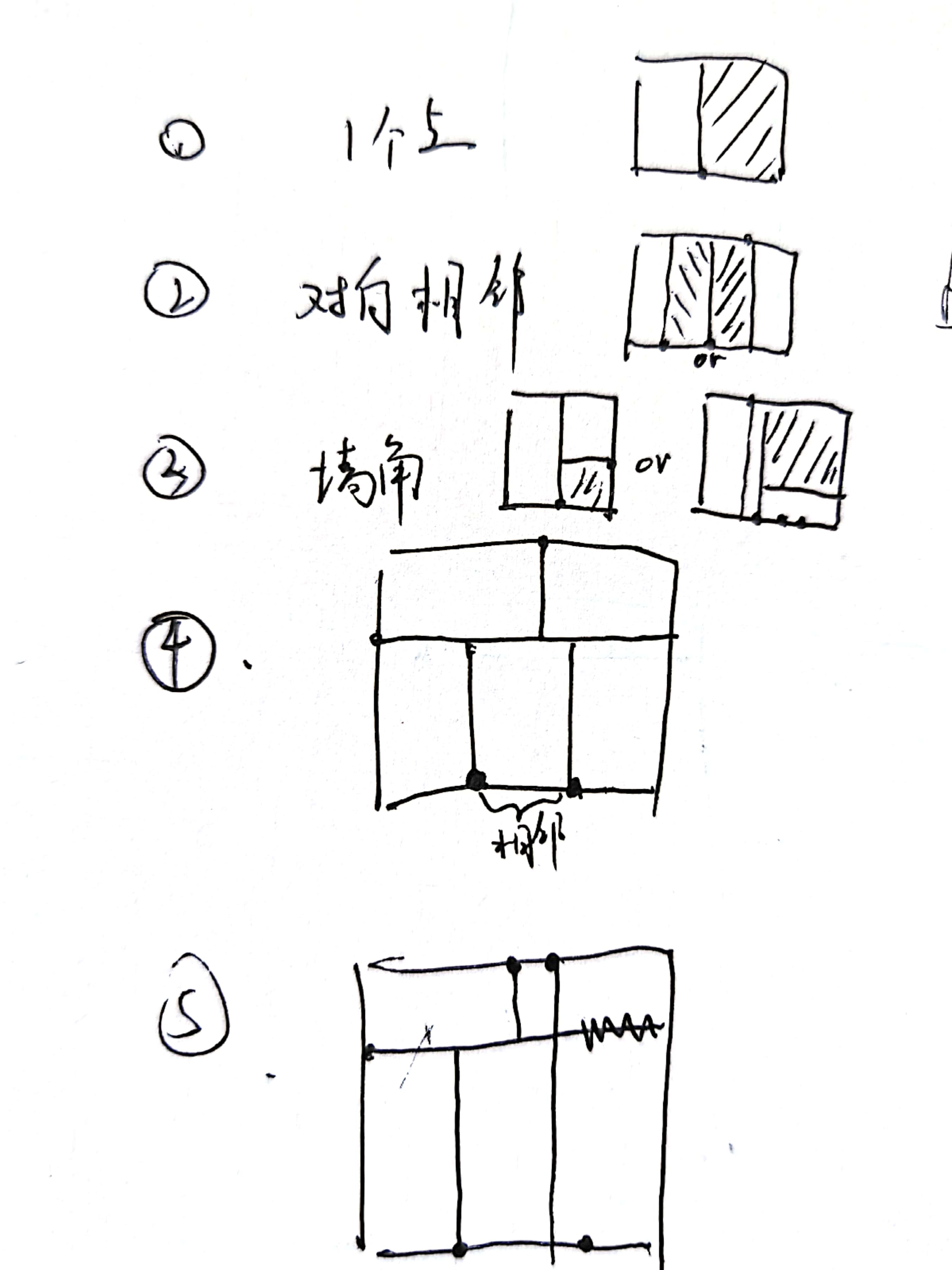
给\(n\)个在矩形\(a\times b\)边上的点,要给所有点分配一个顺序,每个点按顺序作和所在边垂直的线,直到碰到另外一条线或者边。求分割完之后最大的最大子矩形面积。
\(1 \le n \le 10^5,1 \le a,b \le 10^9\)。
题解¶
大分类讨论,懒得写了,可以看题解。
旋转三次,以每条边为底边都讨论一次比较方便。
H¶
solved by TYB
题意¶
略。
题解¶
猜猜迷惑题。
I¶
**upsolved by **
题意¶
题解¶
J¶
upsolved by TYB
题意¶
略。
题解¶
简单推式子分段讨论一下即可。
K¶
solved by ???
题意¶
题解¶
L¶
solved by YZW
题意¶
题解¶
M¶
solved by YZW
题意¶
题解¶
N¶
solved by YZW
题意¶
题解¶
记录¶
YZW写N,WA一次后AC(0:20)。
JLK过D(0:28)。
TYB写K,WA了两次后AC(0:44)。
JLK写A,WA一次后AC(1:07)。
JLK和TYB讨论H,YZW搞L。
TYB写程序验证H可以随便构造,然后过了(1:39)。
YZW开始搞L。期间JLK和TYB想出了C和G。
YZW过L(2:29)。
TYB开始写C,JLK和YZW一起读M,发现不难。
TYB过C(3:23)。
YZW写M,WA一次后AC(3:54)。
JLK写G,WA两次之后发现漏情况,又WA一次后AC(4:58)。
总结¶
Dirt¶
A(-1):式子推错了
G(-3):漏情况
K(-2):没考虑好n=1
M(-1):没考虑好n=1和相邻相同
N(-1):int128输出写错了(0)